Customizing plots

Background

The draw() function in {gratia} was envisaged as a ggplot-based alternative to mgcv:::plot.gam(). As such, it was never intended to allow the sorts of customization that is possible with ggplot() or some other packages that use ggplot() as the plotting layer. This is largely due to the decision to produce multiple separate ggplot() plots for GAMs with multiple smooths, which would subsequently be combined into a single figure on the device, initially using {cowplot} and more recently {patchwork}. Why I did things this way is evident when you consider how we might represent smooths of 3 or 4 variables (which are more common than you might think; consider space-time models via te(x, y, time, d = c(2,1)) or space-depth-time models [think ocean or atmospheric data over space and at depth (height), observed over time] via te(x, y, depth, time, d = c(2, 1, 1))), and which require facets top produce small multiples, which means we can’t use facets to plot separate smooths. Additional complications arise when we consider more complex smooth types, such as splines on the sphere, for which we might want to us different coordinate systems or geoms to best represent the underlying smooth.

Having gone down the root of combining multiple ggplot objects into a single figure, the problem of customizing these plots quickly rears its head. This vignette presents some solutions to the problem of modifying or adding to the plots produced by draw() culminating in an example illustrating how to use {gratia}’s utility functions to produce your own plots from lower-lever components.

Adding layers to plots with the `&` operator

We start by simulating some data and fitting a GAM with four smooth functions

library("gratia")
library("mgcv")
#> Loading required package: nlme
#> This is mgcv 1.9-1. For overview type 'help("mgcv-package")'.
library("ggplot2")
library("dplyr")
#> 
#> Attaching package: 'dplyr'
#> The following object is masked from 'package:nlme':
#> 
#>     collapse
#> The following objects are masked from 'package:stats':
#> 
#>     filter, lag
#> The following objects are masked from 'package:base':
#> 
#>     intersect, setdiff, setequal, union
library("patchwork")

# simulate data
n <- 400
eg1 <- data_sim("eg1", n = n, seed = 1)

# fit model
m <- gam(y ~ s(x0) + s(x1) + s(x2) + s(x3),
  data = eg1, method = "REML")

The default plot produced by draw() is

p <- draw(m)
p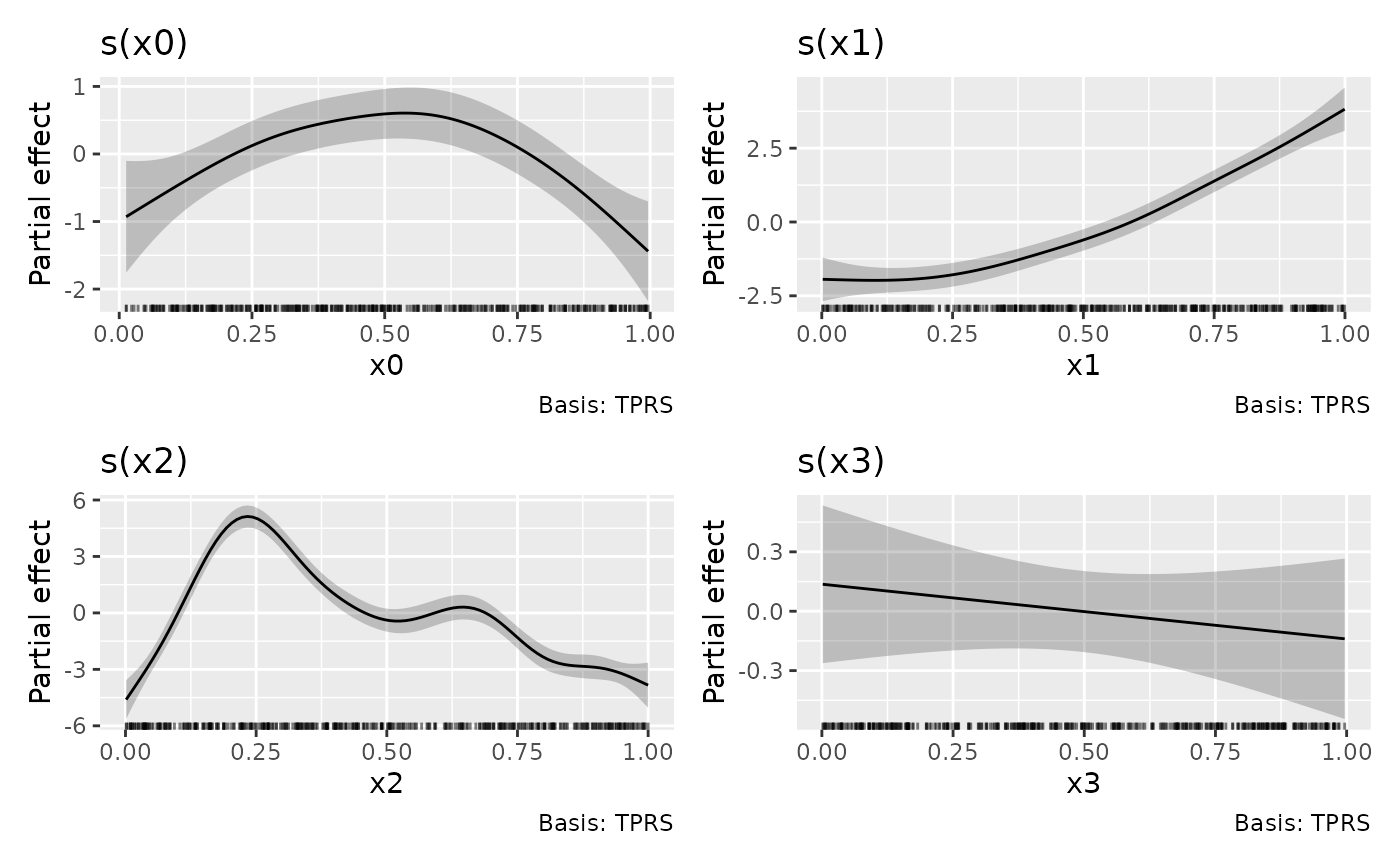

If we want to change the theme for the plots, we can’t append a theme() layer to p as this only affects the last plot in the patchwork¹

p + theme_bw()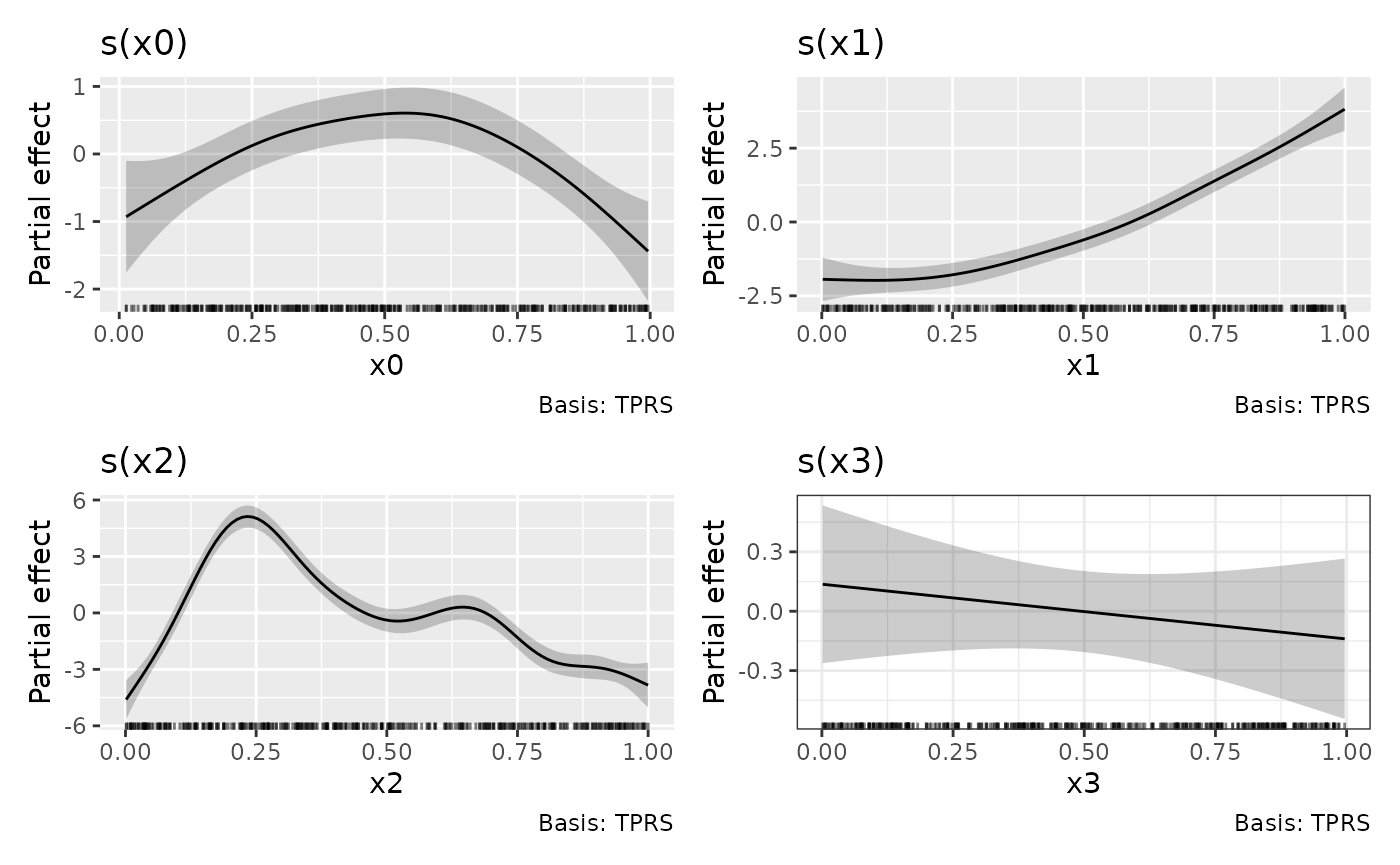

One way to apply the theme to all plots in the patchwork is to the the & operator.

p & theme_bw()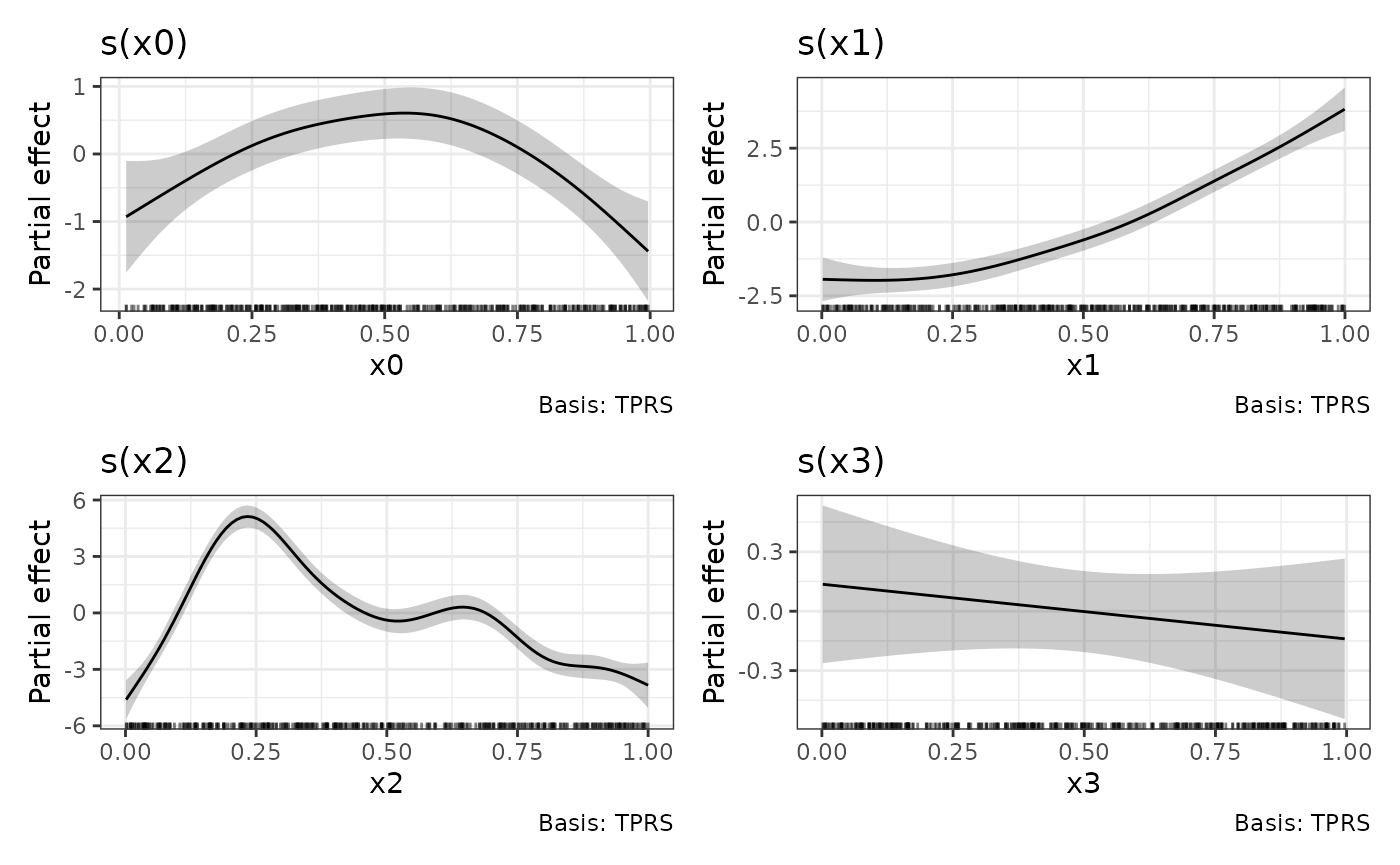

Combining individual plots produced by `draw()`

draw() methods like draw.gam() return an object created by patchwork::wrap_plots(), and as a result it isn’t straightforward to combine those objects into a new patchwork

p1 <- draw(m, select = "s(x0)")
p2 <- draw(m, select = "s(x1)")
p3 <- draw(m, select = "s(x2)")
p1 + p2 + p3
#> Error in `wrap_dims()`:
#> ! Need 3 panels, but together `nrow` and `ncol` only provide 1.
#> ℹ Please increase `ncol` and/or `nrow`.

To avoid the error, we need to use patchwork::plot_layout() to set the dimensions we want

p1 + p2 + p3 + plot_layout(ncol = 3)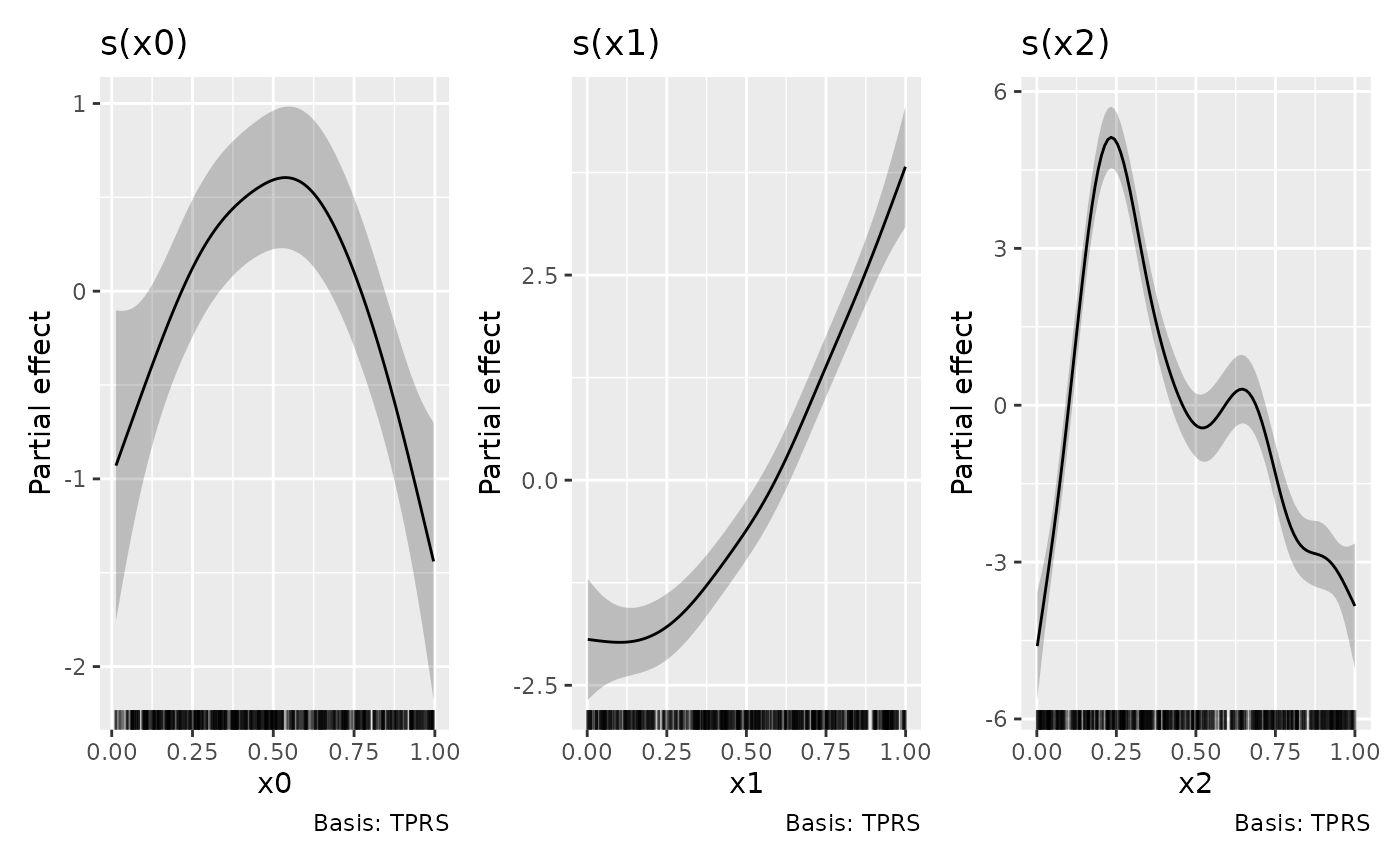

The above could have been achieved directly via draw()

draw(m, select = c("s(x0)", "s(x1)", "s(x2)"), ncol = 3)

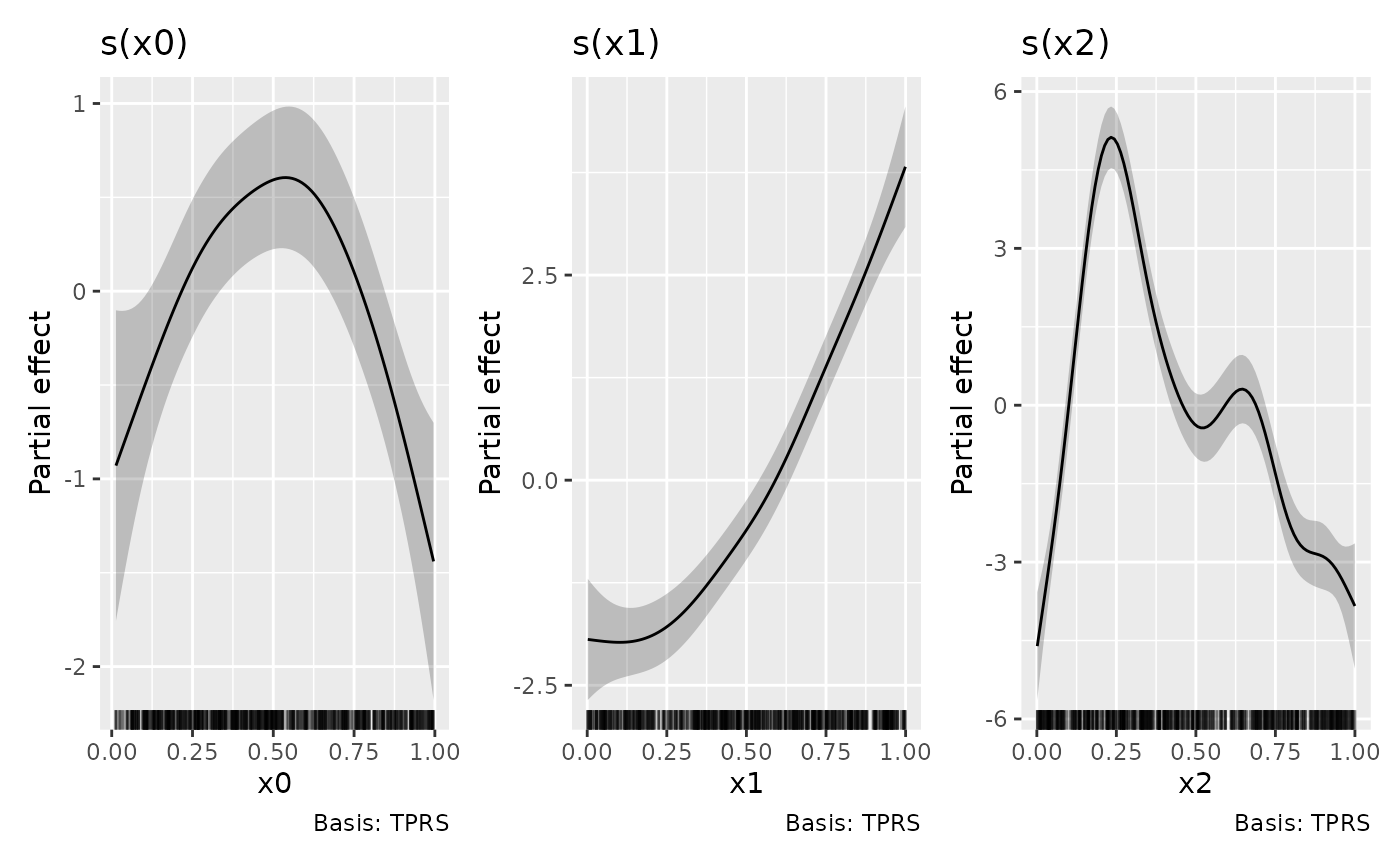
but it is instructive to know how to combine the outputs of draw() should the need arise, such as when you want to create a patchwork of plots from different models.

Building your own plot by hand

{gratia} provides high-level functions like draw() to get you a good graphical overview of a fitted model, but with little option for customisation — it isn’t possible or desirable to allow all possible customisation options and fatures of {ggplot2} through a single function. Think about how many arguments that would require!

Instead, {gratia} also exports the lower-level functions used draw() so that you can create your own plot using whatever {ggplot2} functions make sense. In the next few code blocks we’ll see how the plot created by draw(m) can be recreated by hand using these lower-level building blocks.

The main thing we need is to evaluate the smooths at values of their covariates. This is done using smooth_estimates(). We also need to add a credible interval to the evaluations, which can be done tidyverse-style via add_confint()

# evaluate the smooths
sm <- smooth_estimates(m) |>
  add_confint()
sm
#> # A tibble: 400 × 11
#>    .smooth .type .by   .estimate   .se     x0    x1    x2    x3 .lower_ci
#>    <chr>   <chr> <chr>     <dbl> <dbl>  <dbl> <dbl> <dbl> <dbl>     <dbl>
#>  1 s(x0)   TPRS  NA       -0.929 0.422 0.0131    NA    NA    NA    -1.76 
#>  2 s(x0)   TPRS  NA       -0.881 0.396 0.0230    NA    NA    NA    -1.66 
#>  3 s(x0)   TPRS  NA       -0.834 0.372 0.0329    NA    NA    NA    -1.56 
#>  4 s(x0)   TPRS  NA       -0.786 0.348 0.0429    NA    NA    NA    -1.47 
#>  5 s(x0)   TPRS  NA       -0.738 0.326 0.0528    NA    NA    NA    -1.38 
#>  6 s(x0)   TPRS  NA       -0.690 0.305 0.0627    NA    NA    NA    -1.29 
#>  7 s(x0)   TPRS  NA       -0.643 0.287 0.0727    NA    NA    NA    -1.20 
#>  8 s(x0)   TPRS  NA       -0.595 0.270 0.0826    NA    NA    NA    -1.12 
#>  9 s(x0)   TPRS  NA       -0.548 0.255 0.0925    NA    NA    NA    -1.05 
#> 10 s(x0)   TPRS  NA       -0.501 0.242 0.102     NA    NA    NA    -0.975
#> # ℹ 390 more rows
#> # ℹ 1 more variable: .upper_ci <dbl>

By default draw.gam() will add partial residuals to the partial effects plots. To achieve the same effect, we need to add the partial residuals to the data used to fit the model. This can be done via add_partial_residuals()

# add partial residuals to data
eg1 <- eg1 |>
  add_partial_residuals(m)

This will² add columns with names "s(x0)". "s(x1)", etc. to the data.

names(eg1)
#>  [1] "y"     "x0"    "x1"    "x2"    "x3"    "f"     "f0"    "f1"    "f2"   
#> [10] "f3"    "s(x0)" "s(x1)" "s(x2)" "s(x3)"

Now we have everything we need to recreate the plots created by draw.gam(). In the code block below we filter sm to focus on a specific smooth, here $f(x2)$ ("s(x2)"), then we add

a rug plot of the observed values of x2,
the credible interval around the estimated smooth,
the partial residuals as a point layer,
the estimated smooth as a line layer,
some annotation

p_sx2 <- sm |>
  filter(.smooth == "s(x2)") |>
  ggplot() +
  geom_rug(aes(x = x2),
    data = eg1,
    sides = "b", length = grid::unit(0.02, "npc")
  ) +
  geom_ribbon(aes(ymin = .lower_ci, ymax = .upper_ci, x = x2),
    alpha = 0.2
  ) +
  geom_point(aes(x = x2, y = `s(x2)`),
    data = eg1, cex = 1.5, colour = "steelblue3"
  ) +
  geom_line(aes(x = x2, y = .estimate), lwd = 1.2) +
  labs(y = "Partial effect", title = "s(x2)")
p_sx2

Assuming we repeat the above steps for the other smooths, creating plot objects p_sx0, p_sx1, p_sx2, and p_sx3 (code not shown), we can complete the plot by creating the patchwork with the desired number of rows and columns

p_sx0 + p_sx1 + p_sx2 + p_sx3 + plot_layout(ncol = 2)

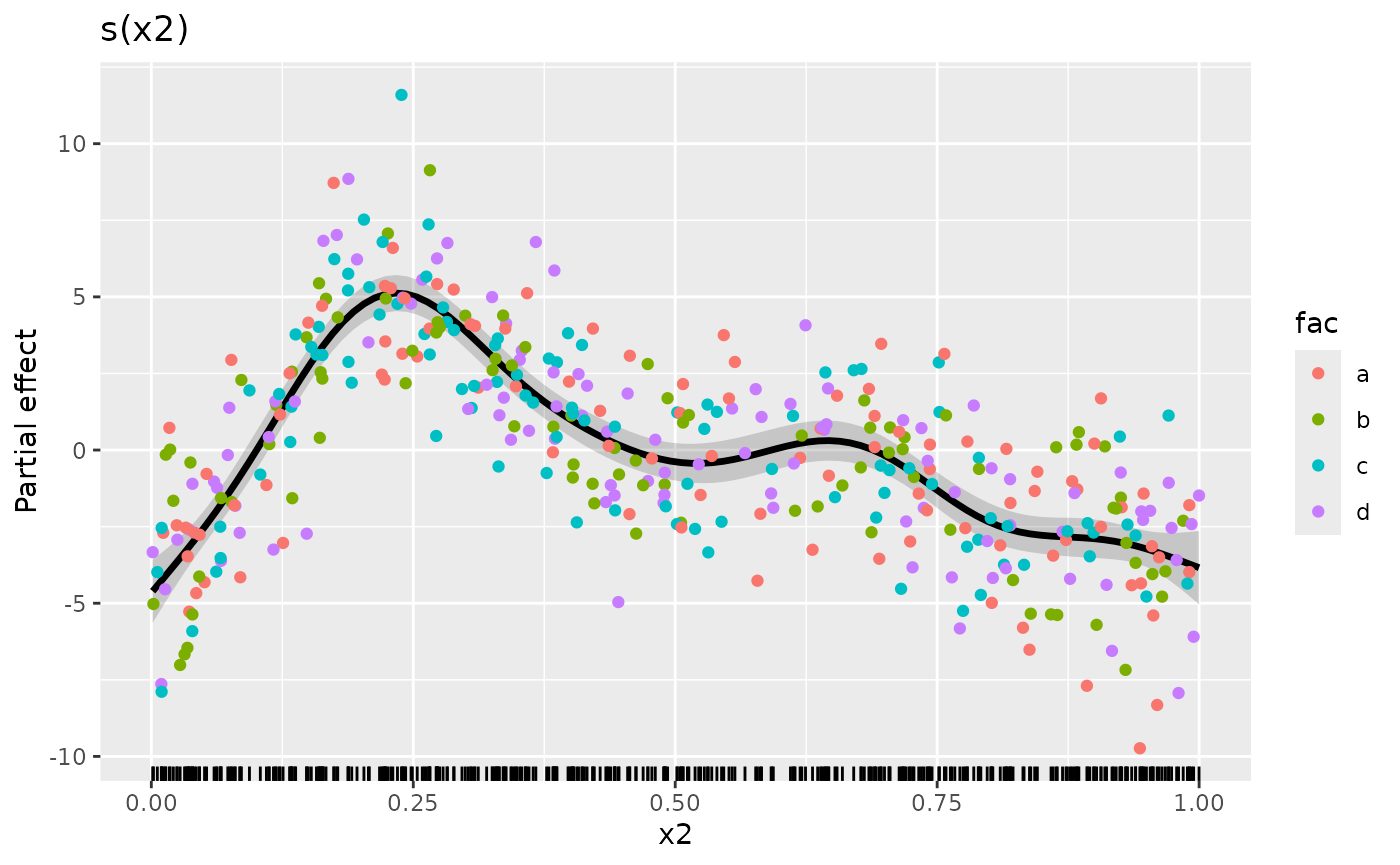
The real benefit of having complete control over how the data are plotted is that you can use the power of {ggplot2} to map additional variables to plot aesthetics. As an example, let’s assume we have a factor variable in the original data and we want to colour the partial residuals according to the levels of this factor. Let’s create that factor

set.seed(12)
eg1 <- eg1 |>
  mutate(fac = sample(letters[1:4], n(), replace = TRUE))

Now we can modify our plotting code to map fac to the colour aesthetic when we plot the partial residuals. To save some typing, we’ll reorder the layers in the plot and add the partial residuals last

plt <- sm |>
  filter(.smooth == "s(x2)") |>
  ggplot() +
  geom_rug(aes(x = x2),
    data = eg1,
    sides = "b", length = grid::unit(0.02, "npc")
  ) +
  geom_ribbon(aes(ymin = .lower_ci, ymax = .upper_ci, x = x2),
    alpha = 0.2
  ) +
  geom_line(aes(x = x2, y = .estimate), lwd = 1.2) +
  labs(y = "Partial effect", title = "s(x2)")

plt +
  geom_point(
    aes(
      x = x2, y = `s(x2)`,
      colour = fac
    ), # <-- map fac to colour aesthetic
    data = eg1, cex = 1.5
  )

We can also do some simple model checking by plotting the smooth with partial residuals coloured according to one of the other covariates (we could also do this by plotting the actual residuals against covariates). In the code chunk below, we map the covariate x1 to both the colour and size aesthetics (note we deleted cex = 1.5 to allow the mapping to size)

plt +
  geom_point(
    aes(
      x = x2, y = `s(x2)`,
      colour = x1, size = x1
    ), # <-- map fac to colour aesthetic
    data = eg1, alpha = 0.3
  ) + # <-- deleted cex!!
  scale_colour_viridis_c(option = "plasma")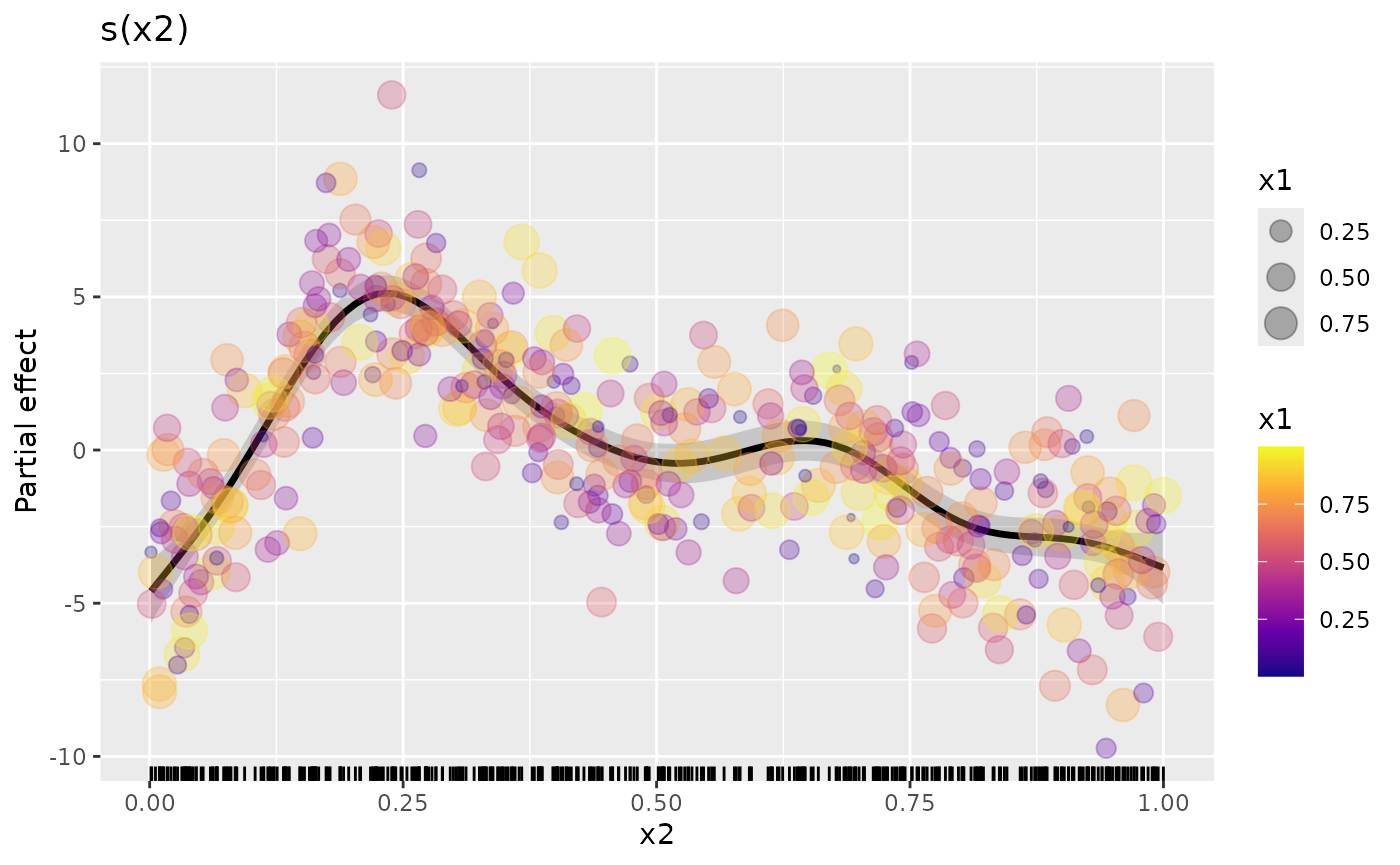

The resulting plot doesn’t show any particular problems with the model because of the way the data were simulated, but hopefully this illustrates what can be possible once you use the low-level functions provided by {gratia}.

Background

Adding layers to plots with the & operator

Combining individual plots produced by draw()

Building your own plot by hand

Adding layers to plots with the `&` operator

Combining individual plots produced by `draw()`