Skip to contents

Posterior draws for individual smooths

Source: R/posterior-samples.R
smooth_samples.Rd

Returns draws from the posterior distributions of smooth functions in a GAM. Useful, for example, for visualising the uncertainty in individual estimated functions.

Usage

smooth_samples(model, ...)

# S3 method for class 'gam'
smooth_samples(
  model,
  select = NULL,
  term = deprecated(),
  n = 1,
  data = newdata,
  method = c("gaussian", "mh", "inla", "user"),
  seed = NULL,
  freq = FALSE,
  unconditional = FALSE,
  n_cores = 1L,
  n_vals = 200,
  burnin = 1000,
  thin = 1,
  t_df = 40,
  rw_scale = 0.25,
  rng_per_smooth = FALSE,
  draws = NULL,
  partial_match = NULL,
  mvn_method = c("mvnfast", "mgcv"),
  ...,
  newdata = NULL,
  ncores = NULL
)

Arguments

model

a fitted model of the supported types

...

arguments passed to other methods. For fitted_samples(), these are passed on to mgcv::predict.gam(). For posterior_samples() these are passed on to fitted_samples(). For predicted_samples() these are passed on to the relevant simulate() method.

select

character; select which smooth's posterior to draw from. The default (NULL) means the posteriors of all smooths in model wil be sampled from. If supplied, a character vector of requested terms.

term

[Deprecated] Use select instead.

n

numeric; the number of posterior samples to return.

data

data frame; new observations at which the posterior draws from the model should be evaluated. If not supplied, the data used to fit the model will be used for data, if available in model.

method

character; which method should be used to draw samples from the posterior distribution. "gaussian" uses a Gaussian (Laplace) approximation to the posterior. "mh" uses a Metropolis Hastings sampler that alternates t proposals with proposals based on a shrunken version of the posterior covariance matrix. "inla" uses a variant of Integrated Nested Laplace Approximation due to Wood (2019), (currently not implemented). "user" allows for user-supplied posterior draws (currently not implemented).

seed

numeric; a random seed for the simulations.

freq

logical; TRUE to use the frequentist covariance matrix of the parameter estimators, FALSE to use the Bayesian posterior covariance matrix of the parameters.

unconditional

logical; if TRUE (and freq == FALSE) then the Bayesian smoothing parameter uncertainty corrected covariance matrix is used, if available.

n_cores

number of cores for generating random variables from a multivariate normal distribution. Passed to mvnfast::rmvn(). Parallelization will take place only if OpenMP is supported (but appears to work on Windows with current R).

n_vals

numeric; how many locations to evaluate the smooth at if data not supplied

burnin

numeric; number of samples to discard as the burnin draws. Only used with method = "mh".

thin

numeric; the number of samples to skip when taking n draws. Results in thin * n draws from the posterior being taken. Only used with method = "mh".

t_df

numeric; degrees of freedom for t distribution proposals. Only used with method = "mh".

rw_scale

numeric; Factor by which to scale posterior covariance matrix when generating random walk proposals. Negative or non finite to skip the random walk step. Only used with method = "mh".

rng_per_smooth

logical; if TRUE, the behaviour of gratia version 0.8.1 or earlier is used, whereby a separate call the the random number generator (RNG) is performed for each smooth. If FALSE, a single call to the RNG is performed for all model parameters

draws

matrix; user supplied posterior draws to be used when method = "user".

partial_match

logical; should smooths be selected by partial matches with select? If TRUE, select can only be a single string to match against.

mvn_method

character; one of "mvnfast" or "mgcv". The default is uses mvnfast::rmvn(), which can be considerably faster at generate large numbers of MVN random values than mgcv::rmvn(), but which might not work for some marginal fits, such as those where the covariance matrix is close to singular.

newdata

Deprecated: use data instead.

ncores

Deprecated; use n_cores instead. The number of cores for generating random variables from a multivariate normal distribution. Passed to mvnfast::rmvn(). Parallelization will take place only if OpenMP is supported (but appears to work on Windows with current R).

Value

A tibble with additional classes "smooth_samples" and `"posterior_samples".

For the "gam" method, the columns currently returned (not in this order) are:

  • .smooth; character vector. Indicates the smooth function for that particular draw,

  • .term; character vector. Similar to smooth, but will contain the full label for the smooth, to differentiate factor-by smooths for example.

  • .by; character vector. If the smooth involves a by term, the by variable will be named here, NA_character_ otherwise.

  • .row; integer. A vector of values seq_len(n_vals), repeated if n > 1L. Indexes the row in data for that particular draw.

  • .draw; integer. A vector of integer values indexing the particular posterior draw that each row belongs to.

  • .value; numeric. The value of smooth function for this posterior draw and covariate combination.

  • xxx; numeric. A series of one or more columns containing data required for the smooth, named as per the variables involved in the respective smooth.

  • Additional columns will be present in the case of factor by smooths, which will contain the level for the factor named in by_variable for that particular posterior draw.

Warning

The set of variables returned and their order in the tibble is subject to change in future versions. Don't rely on position.

Author

Gavin L. Simpson

Examples

load_mgcv()
dat <- data_sim("eg1", n = 400, seed = 2)
m1 <- gam(y ~ s(x0) + s(x1) + s(x2) + s(x3), data = dat, method = "REML")

sms <- smooth_samples(m1, select = "s(x0)", n = 5, seed = 42)
# \donttest{
sms
#> # A tibble: 1,000 x 8
#>    .smooth .term .type .by    .row .draw .value      x0
#>    <chr>   <chr> <chr> <chr> <int> <int>  <dbl>   <dbl>
#>  1 s(x0)   s(x0) TPRS  NA        1     1 -0.357 0.00711
#>  2 s(x0)   s(x0) TPRS  NA        1     2 -0.465 0.00711
#>  3 s(x0)   s(x0) TPRS  NA        1     3 -0.720 0.00711
#>  4 s(x0)   s(x0) TPRS  NA        1     4 -1.27  0.00711
#>  5 s(x0)   s(x0) TPRS  NA        1     5 -1.18  0.00711
#>  6 s(x0)   s(x0) TPRS  NA        2     1 -0.365 0.0121 
#>  7 s(x0)   s(x0) TPRS  NA        2     2 -0.464 0.0121 
#>  8 s(x0)   s(x0) TPRS  NA        2     3 -0.708 0.0121 
#>  9 s(x0)   s(x0) TPRS  NA        2     4 -1.24  0.0121 
#> 10 s(x0)   s(x0) TPRS  NA        2     5 -1.16  0.0121 
#> # i 990 more rows
# }

## A factor by example (with a spurious covariate x0)
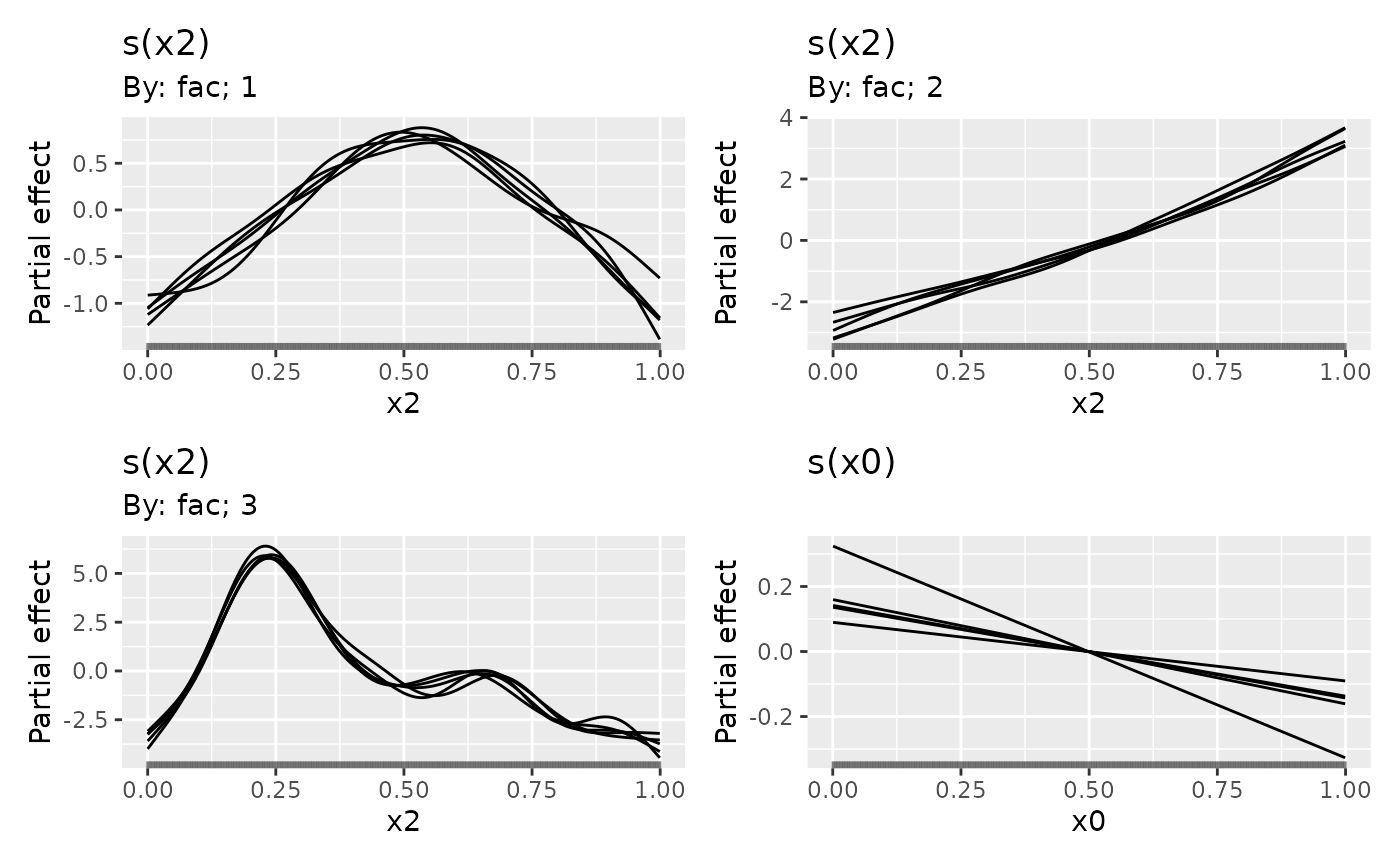
dat <- data_sim("eg4", n = 1000, seed = 2)

## fit model...
m2 <- gam(y ~ fac + s(x2, by = fac) + s(x0), data = dat)
sms <- smooth_samples(m2, n = 5, seed = 42)
draw(sms)