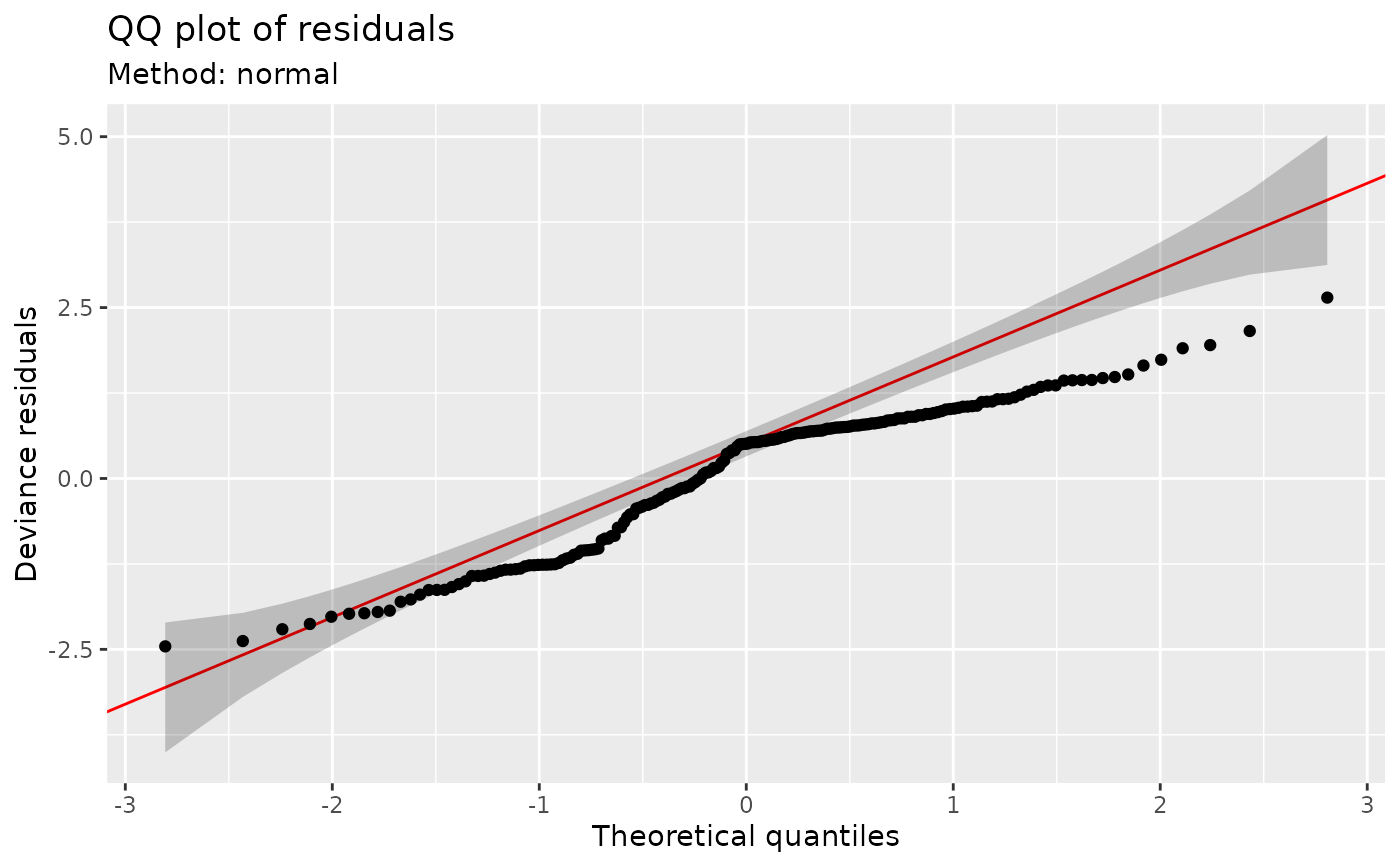
Quantile-quantile plot of model residuals

Quantile-quantile plots (QQ-plots) for GAMs using the reference quantiles of Augustin et al (2012).

Usage

qq_plot(model, ...)

# Default S3 method
qq_plot(model, ...)

# S3 method for class 'gam'
qq_plot(
  model,
  method = c("uniform", "simulate", "normal", "direct"),
  type = c("deviance", "response", "pearson"),
  n_uniform = 10,
  n_simulate = 50,
  seed = NULL,
  level = 0.9,
  ylab = NULL,
  xlab = NULL,
  title = NULL,
  subtitle = NULL,
  caption = NULL,
  ci_col = "black",
  ci_alpha = 0.2,
  point_col = "black",
  point_alpha = 1,
  line_col = "red",
  ...
)

# S3 method for class 'glm'
qq_plot(model, ...)

# S3 method for class 'lm'
qq_plot(model, ...)

Arguments

model

a fitted model. Currently models inheriting from class "gam", as well as classes "glm" and "lm" from calls to stats::glm or stats::lm are supported.

...

arguments passed ot other methods.

method

character; method used to generate theoretical quantiles. The default is "uniform", which generates reference quantiles using random draws from a uniform distribution and the inverse cummulative distribution function (CDF) of the fitted values. The reference quantiles are averaged over n_uniform draws. "simulate" generates reference quantiles by simulating new response data from the model at the observed values of the covariates, which are then residualised to generate reference quantiles, using n_simulate simulated data sets. "normal" generates reference quantiles using the standard normal distribution. "uniform" is more computationally efficient, but "simulate" allows reference bands to be drawn on the QQ-plot. "normal" should be avoided but is used as a fall back if a random number generator ("simulate") or the inverse of the CDF are not available from the family used during model fitting (`"uniform"“).

Note that method = "direct" is deprecated in favour of method = "uniform".

type

character; type of residuals to use. Only "deviance", "response", and "pearson" residuals are allowed.

n_uniform

numeric; number of times to randomize uniform quantiles in the direct computation method (method = "uniform").

n_simulate

numeric; number of data sets to simulate from the estimated model when using the simulation method (method = "simulate").

seed

numeric; the random number seed to use for method = "simulate" and method = "uniform".

level

numeric; the coverage level for reference intervals. Must be strictly 0 < level < 1. Only used with method = "simulate".

ylab

character or expression; the label for the y axis. If not supplied, a suitable label will be generated.

xlab

character or expression; the label for the y axis. If not supplied, a suitable label will be generated.

title

character or expression; the title for the plot. See ggplot2::labs(). May be a vector, one per penalty.

subtitle

character or expression; the subtitle for the plot. See ggplot2::labs(). May be a vector, one per penalty.

caption

character or expression; the plot caption. See ggplot2::labs(). May be a vector, one per penalty.

ci_col

fill colour for the reference interval when method = "simulate".

ci_alpha

alpha transparency for the reference interval when method = "simulate".

point_col

colour of points on the QQ plot.

point_alpha

alpha transparency of points on the QQ plot.

line_col

colour used to draw the reference line.

Note

The wording used in mgcv::qq.gam() uses direct in reference to the simulated residuals method (method = "simulated"). To avoid confusion, method = "direct" is deprecated in favour of method = "uniform".

References

The underlying methodology used when method is "simulate" or "uniform" is described in Augustin et al (2012):

Augustin, N.H., Sauleau, E.-A., Wood, S.N., (2012) On quantile quantile plots for generalized linear models. Computational Statatistics and Data Analysis 56, 2404-2409 doi:10.1016/j.csda.2012.01.026 .

Examples

load_mgcv()
## simulate binomial data...
dat <- data_sim("eg1", n = 200, dist = "binary", scale = .33, seed = 0)
p <- binomial()$linkinv(dat$f) # binomial p
n <- sample(c(1, 3), 200, replace = TRUE) # binomial n
dat <- transform(dat, y = rbinom(n, n, p), n = n)
m <- gam(y / n ~ s(x0) + s(x1) + s(x2) + s(x3),
  family = binomial, data = dat, weights = n,
  method = "REML"
)

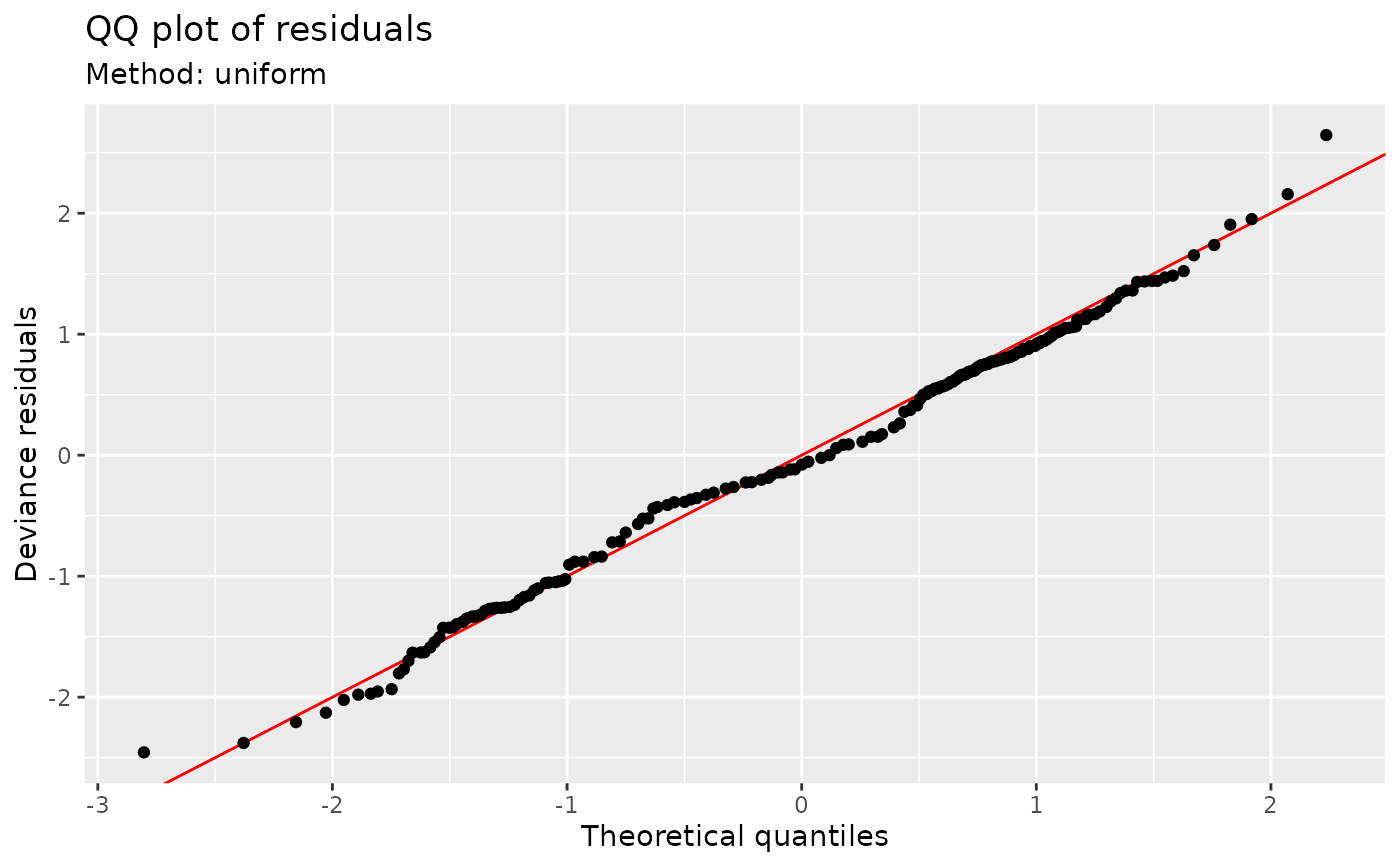
## Q-Q plot; default using direct randomization of uniform quantiles
qq_plot(m)


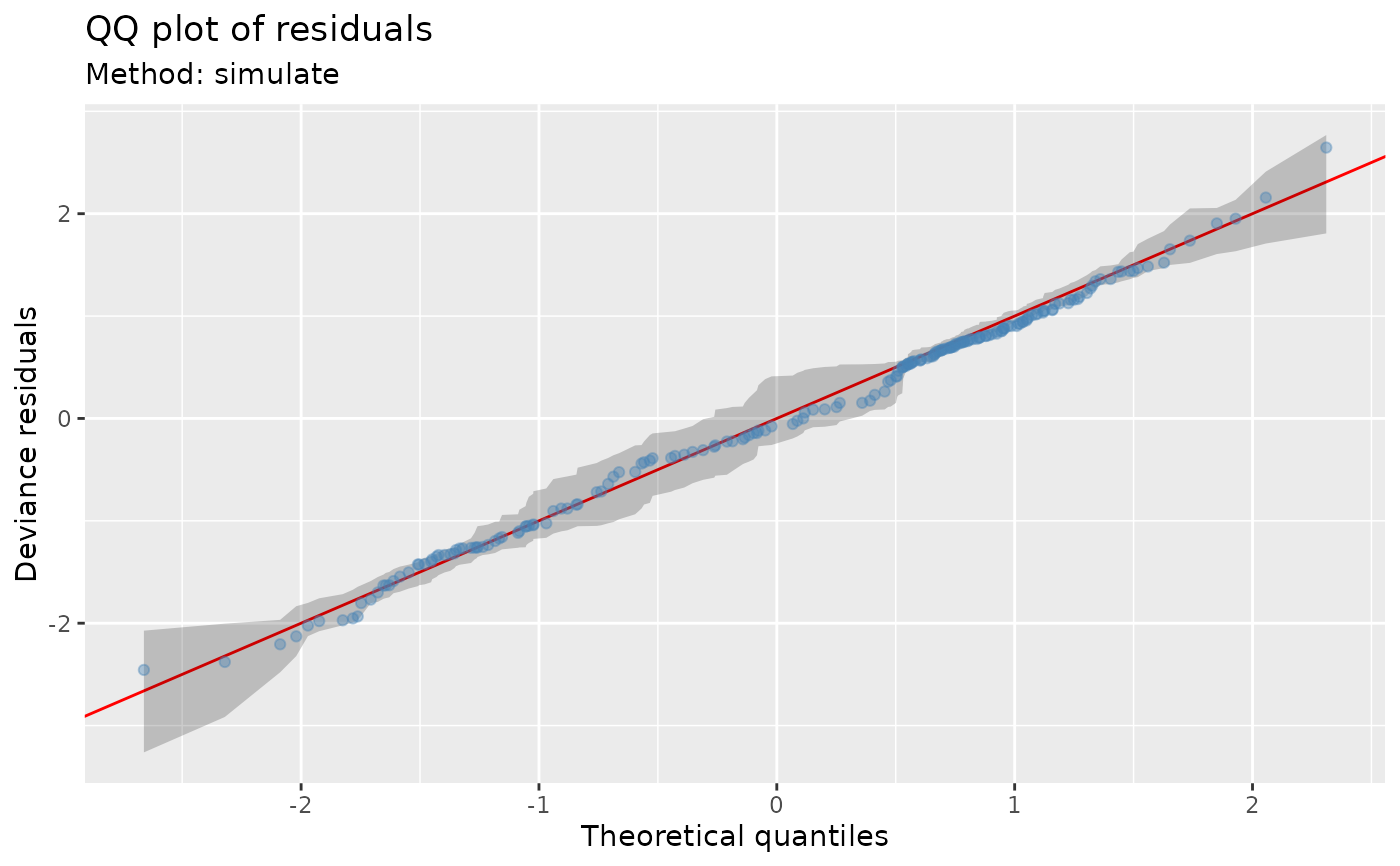
## Alternatively use simulate new data from the model, which
## allows construction of reference intervals for the Q-Q plot
qq_plot(m,
  method = "simulate",
  seed = 42,
  point_col = "steelblue",
  point_alpha = 0.4
)


## ... or use the usual normality assumption
qq_plot(m, method = "normal")